代数 (2) 子代数
#子代数
2023-10-10
子代数,简单来说就是继承原代数的载体和代数常元,原代数的运算在该代数上仍然满足封闭性即可。
子代数定义
要求新载体 \(A'\) 是原载体\(A\) 的子集,运算仍然封闭,且原有的常元仍在 \(A'\)中
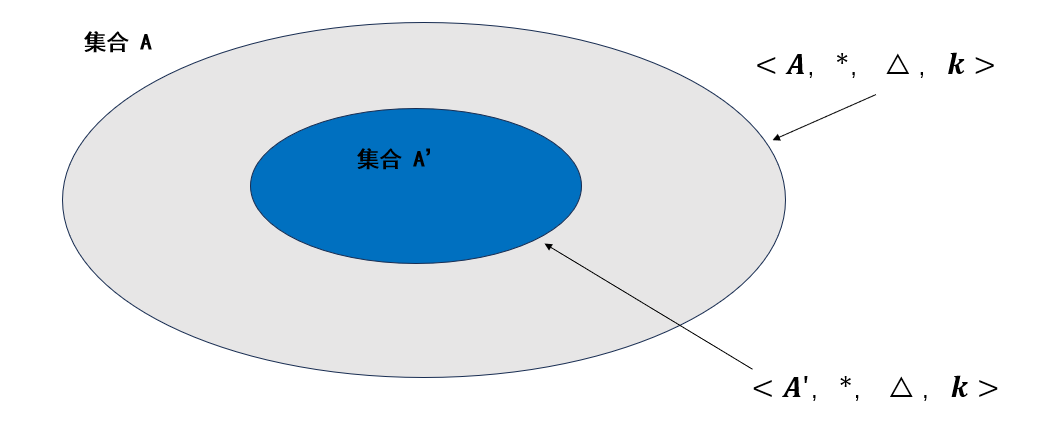
设\(<A,*,△,k>\)是一个代数系统,\(*\)*和\(△\)分别是 载体\(A\)上的二元运算和一元运算,\(k\)是代数常元, 如果满足:
- \(A’⊆A\)
- \(*\)和\(△\)运算在\(A’\)上封闭
- \(k∈A’\),
那么称\(<A',*,△,k>\)是\(<A,*,△,k>\)的子代数。
平凡子代数和非平凡子代数(真子代数),前者要求载体的所有元素都是常元,后者则是除了平凡子代数之外的所有其他子代数